Sigh…I must be crazy.

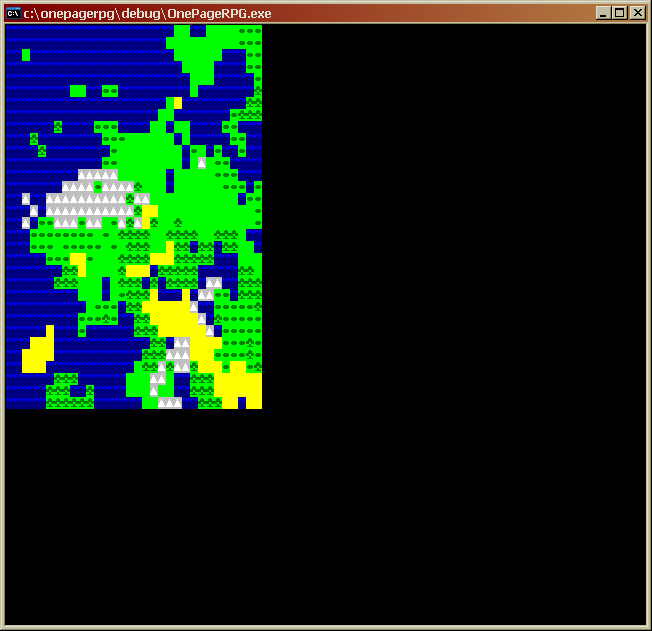
RPGs are just so information dense; doing one in one page seems almost impossible without cutting practically every feature that makes an RPG an RPG. But as you can see, I’m thinking positive…this is basically a much more effective reworking of the terrain generation I started on with 40-Hour RPG #1 (which I failed to complete, if you’ll remember).

Basically, I wanted a algorithm that made maps that reminded me of this. I must use an algorithm, because I want the map to be 64×64 (I don’t think a smaller map will feel big enough to represent a world). If I tried to simply use a data file, I’d waste 4096 bytes just on the world. An algorithm that takes up fewer than 4096 bytes and can generate a random world would be a big win.

I now know what I was doing wrong with my first terrain generator. I walked the Path of Perlin and tried to do a heightfield. I can’t really blame myself; google “random terrain generation” and practically all you will get are articles about heightfields.

You know what? I frigging hate heightfields. For one thing, they are not an accurate representation of how terrain looks. They’re too smooth; too rolling. They say nothing about what type of terrain it is or what is on the terrain, just what elevation it is. And you will never, ever get a realistic-looking river out of a heightfield.

So I went back to a very early idea I had – that of seeding the map grid at regular intervals with terrain types and then having them grow and fight each other for terrain tiles. I effectively walked the Path of Conway instead. This worked much better and started giving me maps that I felt I might be able to use, but I still think there is room for improvement.

My current intention is to include both a world generation algorithm and a dungeon level generation algorithm. I will probably run both until I get results I like and hardcode those seeds so that the player gets known content; otherwise the odds are good that the game would be unfinishable.

I am going to do my best to get it into one page. Going the two-page route here seems like a copout, since I’m almost positive I could do an RPG in two pages. (Especially since Tom is already doing an RPG in two pages. Gosh, it sure would be nice if he’d update his blog with a couple screenshots of it.)

Let’s see what I can do in one.

My first One-Page Game is complete, and I completed the most restrictive challenge – a game in one 80×60 page! And here it is!


#include <windows.h>
#include <vector>
using namespace std;HANDLE wh;HANDLE rh;CHAR_INFO bb[4000];COORD cBS={80,50};
COORD cPos = {0,0};SMALL_RECT wA = {0,0,79,49};bool running=true;int fc = 0;
struct u{int x;int y;int dx;int dy;int state;};vector<u> c;vector<u> mush;
vector<u> bullets;u s = {20, 49, 0, 0, 1};int score,lives,i,j;SetChar(int x,
int y,char c,int a){bb[(y*80)+x].Char.AsciiChar=c;bb[(y*80)+x].Attributes=a;}
void ResetC(){c.clear();u head={19,0,1,1,1};c.push_back(head);for(i=18;i>=0;--i)
{u b={i,0,0,0,0};c.push_back(b);}}SetPos(int x,int y){COORD c1={x,y};
SetConsoleCursorPosition(wh,c1);}MoveCP(){if(fc%2){for(i=19;i>-1;--i){int headx,
heady;if(c[i].state==1){int tx=c[i].x+c[i].dx;bool hm=false;for(j=0;j<
mush.size();++j){if(c[i].x+c[i].dx==mush[j].x&&c[i].y==mush[j].y&&mush[j].state)
hm=true;}if(tx>40||tx<0||hm){c[i].dx=-c[i].dx;int ty=c[i].y+c[i].dy;if(ty>49||
ty<0||(ty<39&&c[i].dy==-1)){c[i].dy=-c[i].dy;}c[i].y+=c[i].dy;}else{c[i].x+=
c[i].dx;}}else{c[i].x=c[i-1].x;c[i].y=c[i-1].y;}}}}MoveS(){bool ok=true;for(i=0;
i<mush.size();++i){if(s.dx==mush[i].x&&s.dy==mush[i].y)ok=false;}if(ok){s.x=
s.dx;s.y = s.dy;}}MoveB(){for(j=0;j<2;++j){for(i=0;i<20;++i){int mrx,mry;
if(c[i].state==1){mrx=c[i].dx;mry=c[i].dy;}if(bullets[j].x==c[i].x&&bullets[j].y
==c[i].y&&bullets[j].state!=0&&c[i].state!=-1){if(c[i].state==0)score+=10;else
score+=50;u m={c[i].x,c[i].y,0,0,1};mush.push_back(m);bullets[j].state=0;
c[i].state=-1;if(i!= 19){if(c[i+1].state!=-1){c[i+1].state=1;c[i+1].dx=mrx;
c[i+1].dy = mry;}}int lc=0;for(int z=0;z<20;++z){if(c[z].state!=-1)++lc;}
if(lc==0)ResetC();}}for(i=0;i<mush.size();++i){if(bullets[j].x==mush[i].x&&
bullets[j].y==mush[i].y&&bullets[j].state!=0&&mush[i].state==1){bullets[j].state
=0;mush[i].state=0;score+=3;}}if(bullets[j].state==1){--bullets[j].y;
if(bullets[j].y < 0)bullets[j].state=0;}}}Init(){wh=GetStdHandle(
STD_OUTPUT_HANDLE);rh=GetStdHandle(STD_INPUT_HANDLE);SMALL_RECT w={0,0,79,49};
SetConsoleWindowInfo(wh,TRUE,&w);COORD b={80,50};SetConsoleScreenBufferSize(wh,
b);}Input(){DWORD nE=0;DWORD nER=0;GetNumberOfConsoleInputEvents(rh,&nE);if(nE!=
0){INPUT_RECORD *eB=new INPUT_RECORD[nE];ReadConsoleInput(rh,eB,nE,&nER);for(i=
0;i<nER;++i){if (eB[i].EventType==KEY_EVENT){if(eB[i].Event.KeyEvent.
wVirtualKeyCode==VK_ESCAPE){running=false;}}else if(eB[i].EventType==
MOUSE_EVENT){s.dx=eB[i].Event.MouseEvent.dwMousePosition.X;if(s.dx>40)s.dx=40;
s.dy=eB[i].Event.MouseEvent.dwMousePosition.Y;if(s.dy<40)s.dy=40;if(eB[i].Event.
MouseEvent.dwButtonState&FROM_LEFT_1ST_BUTTON_PRESSED){for(int z=0;z<2;++z){
if(bullets[z].state == 0){bullets[z].x=s.x;bullets[z].y=s.y-1;bullets[z].state
=1;break;}}}}}delete eB;}}ResetM(){mush.clear();for(i=0;i<100;++i){u m={rand()
%40,(rand()%46)+1,0,0,1};mush.push_back(m);}}int main(int argc,char* argv[])
{Init();ResetC();ResetM();u b1={ -1, -1, 0, 0, 0};bullets.push_back(b1);bullets.
push_back(b1);score=0;lives=3;while(running){ZeroMemory(bb,4000*sizeof(
CHAR_INFO));Input();MoveCP();MoveS();MoveB();for(i=0;i<50;++i)SetChar(41,i,219,
15);SetChar(s.x,s.y,127,15);for(i=0;i<20;++i){if(c[i].state==1){SetChar(c[i].x,
c[i].y,1,2);}else if(c[i].state==0){SetChar(c[i].x,c[i].y,15,2);}}for(i=0;i<
mush.size();++i){if(mush[i].state){SetChar(mush[i].x,mush[i].y,6,14);}}for(i=0;
i<2;++i){if(bullets[i].state)SetChar(bullets[i].x,bullets[i].y,24,15);}
WriteConsoleOutput(wh,bb,cBS,cPos,&wA);bool ll=false;for(i=0;i<c.size();++i){
if(c[i].state!=-1&&c[i].x==s.x&&c[i].y==s.y){--lives;ll=true;ResetC();}}int mc
=0;for(i=0;i<mush.size();++i)if(mush[i].state)++mc;if(mc<50){int nm=0;do{nm=
rand()%mush.size();}while(mush[nm].state);mush[nm].state=1;}SetPos(45,0);printf(
"SANDWORM!");SetPos(45,1);printf("Score: %d",score);SetPos(45,2);printf(
"Lives: %d",lives);if(!lives){SetPos(16,20);printf("GAME OVER");Sleep(5000);
score=0;lives=3;ResetM();}else if(ll)Sleep(1000);else Sleep(17);++fc;}return 0;}


Create a new console application project in Visual Studio, paste that into the source file, and compile it. If you have trouble compiling the file, it might be easier to debug if you had a cleaner version – so here’s one.

Or, if that’s too much trouble, you can just download the executable.

The game is a simplified version of the classic arcade game Centipede. You control your shooter with the mouse and fire with the left mouse button. Shooting the sandworm creates a new rock and splits the sandworm into two separate parts. Breaking a rock gets you three points, hitting a sandworm segment gets you ten points, and hitting a sandworm head gets you fifty points. You can have up to two shots on the screen at the same time. If you manage to kill the entire sandworm, a new one respawns. If any part of the sandworm hits you, you lose a life. Lose all your lives and it’s game over, but a new game will start in a few seconds automatically. Press ESC on your keyboard to exit the game. Press ALT + ENTER to play in fullscreen mode.

Here I’ve chopped the sandworm up into sushi…I’m probably going to regret that in a few minutes.

I was quite nervous about coming in under the limit because of the incredibly long function and constant names Windows insists on using. I was surprised when I did the final compress to see that I had a full eight lines free, more than enough space to put in another feature like the spider or the flea! But this will do for a first version.

Needless to say, the code is filthy. You may have problems on other platforms with the fact that I don’t declare return values for a lot of my functions (VS 2003 supplies int automatically) and use variables without initializing them first. And if you’re not on Windows…well, good luck 🙂

So, challenge successfully accomplished! I just wish Tom would get off his duff and complete his two-page 3D RPG…you will NOT believe your eyes when you see it.

For my next challenge, I will almost certainly attempt an RPG in one page of source. But it’s not like I’m obsessed with RPGs or anything…